(R) Survival Analysis - Kaplan-Meier and Cox Models (SPSS)

Survival Analysis is a statistical methodology which measures the probability of an event occurring within a group over a period of time.

If you have a decent understanding of the linear regression concept, understanding the output generated by the survival analysis model is fairly simple.

We will demonstrate the methodology of survival analysis through various examples. The data set which will be utilized for the following demonstrations is found within the R “survival” package.

Example: Survival Analysis - Kaplan-Meier Model (R)

# With the R package: “survival” downloaded and enabled #

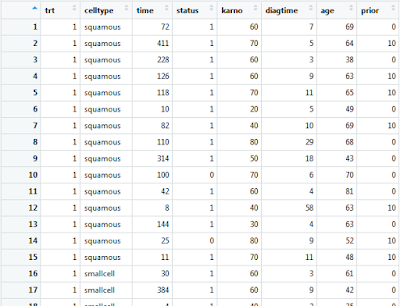
The R “survival” package comes with the “veteran” data frame embedded within its composition. With the “survival” package enabled, the “veteran” data frame can be called with the command: “veteran”.

If you wish to view this data frame within the R-Studio graphical user interface, you must first assign it to a native data frame variable.

vet1 <- veteran

Double clicking on this data frame variable within the environment frame of R-Studio will present you with the following:

To begin performing a Kaplan-Meier survival analysis within the R platform, you must utilize the following line of code:

kmsurvival <- survfit(Surv(time, status) ~ 1, data=vet1)

This code will indicate to R that a Kaplan-Meier survival analysis should be embarked upon. The “time” variable is indicating the time status, and the “status” variable is indicating censor status (1 = Non-Censored, 0 = Censored). In the case of this particular model, both data frame variables are named exactly what the variable type implies. Please be aware that data frames variables are not always perfectly assigned in this manner.

To view the model output, we will invoke the following function:

summary(kmsurvival)

Which produces the following output:

> summary(kmsurvival)
Call: survfit(formula = Surv(time, status) ~ 1, data = vet1)

time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 137 2 0.985 0.01025 0.96552 1.0000
2 135 1 0.978 0.01250 0.95390 1.0000
3 134 1 0.971 0.01438 0.94302 0.9994
4 133 1 0.964 0.01602 0.93261 0.9954
7 132 3 0.942 0.02003 0.90315 0.9817
8 129 4 0.912 0.02415 0.86628 0.9610
10 125 2 0.898 0.02588 0.84850 0.9500
11 123 1 0.891 0.02668 0.83973 0.9444
12 122 2 0.876 0.02817 0.82241 0.9329
13 120 2 0.861 0.02953 0.80534 0.9212
15 118 2 0.847 0.03078 0.78849 0.9092
16 116 1 0.839 0.03137 0.78013 0.9032
18 115 3 0.818 0.03300 0.75533 0.8848
19 112 2 0.803 0.03399 0.73900 0.8724
20 110 2 0.788 0.03490 0.72280 0.8598

The output itself is much greater in length but I have only included the first 20 observations.

In discussing each unique aspect of the output:

time – This variable illustrates the categorical point in time when a measurement was taken.

n.risk – This variable represents the number of individuals remaining within the initial group of measured individuals.

n.event – This variable represents the total number of individuals who were removed from the remaining group of individuals at the measured point in time.

survival – The probability of any individual within the initial group being a remaining member of the group at this present point in time.

Typically, with survival analysis, the application of the methodology is demonstrated through examples pertaining to drug trials. We could imagine, a scenario which involves patients undergoing treatment for some ailment until their symptoms subside. This gradual diminishment of initial individuals involved in the study is illustrated in the output below:

As the categorical measurement of time progresses (63 – 72), the n.risk figure decreases (72 – 71), this is demonstrated by the number of individuals who no longer meet the initial groups classification (n.event = 1). However, how can we explain the phenomenon in which more individuals leave the study than are not accounted for? This is the case for the numerical values encircled in blue.

You may recall earlier, that we specified for the variable “status” within our “survfit” function. What does this variable connotate within the context of our original data frame?

Censoring

As it pertains to survival analysis, the term “censoring” refers to the event in which an individual leaves the original group without the measured even occurring. For example, in the case of a study, this could occur if an individual stops corresponding with the researchers. Or for a more morbid example, if an individual passes away as a result of circumstance un-related to the study.

In either situation, this non-event loss of individuals from the initial group will be connotated by a cross marking on the graphed output. These individuals are considered “censored” individuals.

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled #

autoplot(kmsurvival)

Which produces the following output:

The center solid line represents the survival probability of the model, the outside grey area represents the 5% and 95% confidence intervals. The cross markings on the solid central line indicate an instance when censoring took place.

Example: Survival Analysis - Kaplan-Meier Model (R)

We will now produce a model which contains the same parameters of the previous model. The graphical output created as a result of such is the product of two separate sets of analysis, each set specifying a pre-determined condition. Each conditional scenario will be illustrated within the model output as separate solid lines.

To achieve this desired results, we must run the following lines of code:

# With the R package: “survival” downloaded and enabled #

# In this case, our factor is “trt” #

kmsurvival <- survfit(Surv(time, status) ~ trt, data=vet1)

To view the model output, we will invoke the following function:

summary(kmsurvival)

Which produces the following output:

Call: survfit(formula = Surv(time, status) ~ trt, data = vet1)
trt=1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
3 69 1 0.9855 0.0144 0.95771 1.000
4 68 1 0.9710 0.0202 0.93223 1.000
7 67 1 0.9565 0.0246 0.90959 1.000
8 66 2 0.9275 0.0312 0.86834 0.991
10 64 2 0.8986 0.0363 0.83006 0.973
11 62 1 0.8841 0.0385 0.81165 0.963
12 61 2 0.8551 0.0424 0.77592 0.942
13 59 1 0.8406 0.0441 0.75849 0.932
16 58 1 0.8261 0.0456 0.74132 0.921
18 57 2 0.7971 0.0484 0.70764 0.898
20 55 1 0.7826 0.0497 0.69109 0.886

(and)

trt=2
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 68 2 0.9706 0.0205 0.93125 1.000
2 66 1 0.9559 0.0249 0.90830 1.000
7 65 2 0.9265 0.0317 0.86647 0.991
8 63 2 0.8971 0.0369 0.82766 0.972
13 61 1 0.8824 0.0391 0.80900 0.962
15 60 2 0.8529 0.0429 0.77278 0.941
18 58 1 0.8382 0.0447 0.75513 0.930
19 57 2 0.8088 0.0477 0.72056 0.908
20 55 1 0.7941 0.0490 0.70360 0.896

Again, I shortened the output to conserve space. However, as is evident within the portions of output, each particular condition is illustrated above the conditional output type. (trt = 1, trt = 2)

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled # 

autoplot(kmsurvival)

Which produces the following output:

Notice that in this case, two separate confidence interval areas have been produced, each pair existing as an aspect of the solid line in which it engulfs.

Example: Survival Analysis – Cox Proportional Hazard Model (R)

The Cox Proportional Hazard Model, like the Kaplan-Meier Model, is also a survival analysis methodology. The Cox Model is more complicated in its composition as it allows for the inclusion of additional variables. The inclusion of these additional variables, if correctly integrated, can yield a more descriptive model. However, as a consequence of the model’s complication, the additional aspects which provide positive differentiation, can also lead to the increased probability of user error.

To create a Cox Proportional Hazard Model, we will utilize the following lines of code:

# With the R package: “survival” downloaded and enabled #

coxsurvival <- coxph(Surv(time, status) ~ trt + karno + diagtime + age + prior , data=vet1)

summary(coxsurvival)

This produces the output:

Call:
coxph(formula = Surv(time, status) ~ trt + karno + diagtime +
age + prior, data = vet1)

n= 137, number of events= 128

coef exp(coef) se(coef) z Pr(>|z|)
trt 0.193053 1.212947 0.186446 1.035 0.300
karno -0.034084 0.966490 0.005341 -6.381 1.76e-10 ***
diagtime 0.001723 1.001725 0.009003 0.191 0.848
age -0.003883 0.996125 0.009247 -0.420 0.675
prior -0.007764 0.992266 0.022152 -0.350 0.726
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

exp(coef) exp(-coef) lower .95 upper .95
trt 1.2129 0.8244 0.8417 1.7480
karno 0.9665 1.0347 0.9564 0.9767
diagtime 1.0017 0.9983 0.9842 1.0196
age 0.9961 1.0039 0.9782 1.0143
prior 0.9923 1.0078 0.9501 1.0363

Concordance= 0.714 (se = 0.03 )
Rsquare= 0.271 (max possible= 0.999 )
Likelihood ratio test= 43.27 on 5 df, p=3.259e-08
Wald test = 44.88 on 5 df, p=1.537e-08
Score (logrank) test = 47.39 on 5 df, p=4.734e-09

Primarily, when analyzing the model summary data, we should concern ourselves with the portions of the output which I have highlighted in bold. The initial portion of the output provides values, which are found within the rightmost column, which indicate the strength of each variable as it impacts the overall outcome of the model (Pr(>|z|).

The p-value of the Wald Test (1.537e-08 < .05), indicates that the model is significant. While the r-squared value (.271), indicates that the model is not a particularly good fit as it pertains to the existing data points.

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled # 

coxsurvival <- survfit(coxsurvival)

autoplot(coxsurvival)

Which produces the following output:

Example: Survival Analysis – Cox Proportional Hazard Model with Time Dependent Co-Variates (R) 

There may be instances in which you will encounter survival data which contains time dependent co-variates. What this translates to, in simpler terms, is that the data which you are preparing to analyze contains variables which are dependent on time duration.

The data in these scenarios is typically organized in a manner similar to data presented below:

As is demonstrated within the data set, individuals have been surveyed multiple times. This method has been utilized to account for the variables “symphtomA” and “symphtomB”, which typically occur as a result of the treatment methods occurring over set intervals of time.

It may appear that the time intervals are overlapping in the above example, however, this is not the case. When setting up data for analysis in the manner, it must be structured similarly, with duration aspects appearing to overlap. The lack of ambivalence is due to measurements being taken at the end of each interval. So, in the case of ID:3, measurements were taken at day 50, day 100, day 150, day 200, and day 250.

To begin performing a Cox Proportional Hazard Model with Time Dependent Co-Variates within the R platform, you must utilize the following lines of code:

(I am aware that this sample data, model, and graphical output are equally awful. However, I could not find a worthwhile example to demonstrate, and making data sets from scratch which contain decent representational entries is extremely difficult. The .csv file utilized to create this example can be found at the end of the article.)

coxsurvival1 <- coxph(Surv(time1, time2, status) ~ trt + karno + diagtime + age + symphtomA + symphtomB , data=vet2)

summary(coxsurvival1)

This produces the output:

Call:
coxph(formula = Surv(time1, time2, status) ~ trt + karno + diagtime +
age + symphtomA + symphtomB, data = vet2)

n= 22, number of events= 21

coef exp(coef) se(coef) z Pr(>|z|)
trt 3.959e-16 1.000e+00 1.225e+00 0.000 1.000
karno -2.636e-17 1.000e+00 8.672e-02 0.000 1.000
diagtime -1.281e-16 1.000e+00 1.713e-01 0.000 1.000
age 2.730e-17 1.000e+00 5.009e-02 0.000 1.000
symphtomA -9.177e-16 1.000e+00 7.906e-01 0.000 1.000
symphtomB -1.985e+01 2.392e-09 1.510e+04 -0.001 0.999

exp(coef) exp(-coef) lower .95 upper .95
trt 1.000e+00 1.00e+00 0.09061 11.036
karno 1.000e+00 1.00e+00 0.84370 1.185
diagtime 1.000e+00 1.00e+00 0.71474 1.399
age 1.000e+00 1.00e+00 0.90649 1.103
symphtomA 1.000e+00 1.00e+00 0.21236 4.709
symphtomB 2.392e-09 4.18e+08 0.00000 Inf

Concordance= 1 (se = 1.594 )
Rsquare= 0.118 (max possible= 0.723 )
Likelihood ratio test= 2.77 on 6 df, p=0.8368
Wald test = 0 on 6 df, p=1
Score (logrank) test = 1.78 on 6 df, p=0.9389

To create a graphical output for our example model, we would utilize the following code:

# With the R package: “survival” downloaded and enabled #

coxsurvival1 <- survfit(coxsurvival1)

autoplot(coxsurvival1)

Which produces the following output:

Example: Survival Analysis - Kaplan-Meier Model (SPSS)

To re-create this example, you must first export the “veteran” data set to a .csv file, and then subsequently import it into the SPSS platform.

The result of such should resemble the following:

To begin, you must first select “Analyze” from the upper left drop down menu, then select “Survival”, followed by “Kaplan-Meier”.

This should present the following interface:

Utilizing the top center arrow, designate the variable “time” as the “Time” entry. Then, utilize the second topmost arrow to designate the variable “status” as the “Status” entry.

Once this step has been completed, click on the box labeled “Define Event”.

From the sub-menu generated, input “1” as the “Single value”, then click “Continue”.

Next, click on the menu box labeled “Options”.

This should cause the following menu to populate:

Be sure to check the boxes to the left of the “Mean and medial survival” and “Survival” options.

Once this is completed, click “Continue”, and then click “OK”.

This s will generate the following output:

The model parameters can be modified in the initial menu to produce an output which is differentiated by a factor variable.

This modification would produce the output:

Example: Survival Analysis – Cox Proportional Hazard Model (SPSS)

We will be utilizing the same data set which analyzed in the previous example:

To begin, you must first select “Analyze” from the upper left drop down menu, then select “Survival”, followed by “Cox Regression”.

This should present the following interface:

Utilizing the top center arrow, designate the variable “time” as the “Time” entry. Then, utilize the second topmost arrow to designate the variable “status” as the “status” entry. Finally, utilize the middle center arrow to designate the variables “trt”, “karno”, “diagtime”, “age”, and “prior” as “Covariates”.

Once this step has been completed, click on the box labeled “Define Event”.

From the sub-menu generated, input “1” as the “Single value”, then click “Continue”.

Next, click on the menu option labeled “Plots”.

Within this interface, select the box to the left of the option labeled “Survival”, then click “Continue”.

Once this has been completed click “OK”.

This should produce the following output:

Survival Analysis – Cox Proportional Hazard Model Example File (.csv)

id,trt,celltype,time1,time2,status,karno,diagtime,age,prior,symphtomA,symphtomB
1,1,squamous,0,50,1,60,7,69,0,0,0
1,1,squamous,50,100,1,60,7,69,0,1,0
2,1,squamous,0,50,1,70,5,64,10,1,0
2,1,squamous,50,100,1,70,5,64,10,0,0
2,1,squamous,100,150,1,70,5,64,10,1,0
2,1,squamous,150,200,1,70,5,64,10,1,0
2,1,squamous,200,250,1,70,5,64,10,1,0
2,1,squamous,250,300,1,70,5,64,10,1,0
2,1,squamous,300,350,1,70,5,64,10,1,1
2,1,squamous,350,400,1,70,5,64,10,1,1
2,1,squamous,400,450,1,70,5,64,10,1,1
3,2,squamous,0,50,1,60,3,38,0,0,0
3,2,squamous,50,100,1,60,3,38,0,1,0
3,2,squamous,100,150,1,60,3,38,0,1,0
3,2,squamous,150,200,1,60,3,38,0,1,0
3,2,squamous,200,250,1,60,3,38,0,1,0
4,2,squamous,0,50,1,60,9,63,10,0,0
4,2,squamous,50,100,1,60,9,63,10,1,0
4,2,squamous,100,150,1,60,9,63,10,1,0
5,1,squamous,0,50,1,70,11,65,10,0,0
5,1,squamous,50,100,1,70,11,65,10,0,0
5,1,squamous,100,150,0,70,11,65,10,0,1

That’s all for now, Data Heads! Stay tuned for more informative content!