(R) Why Economic Forecasts are Nonsense

 

I’m tired of witnessing the infestation of financial news sources by prognostication. 

So in today’s entry, we will test for correlation between common financial variables.

Why do these ghosts continue to haunt the thoughts of otherwise rational readers? Perhaps it's the illusion of control. Or perhaps, it’s a desire to be in possession of exclusive knowledge. Knowledge which grants a higher status to those whom possess it. Or maybe it’s a way of justifying one’s superiority. A survivorship bias of sorts. 

The truth is that all economic prediction models are fundamentally flawed. As their predictive capacity is always assessed post-hoc. 

That also holds true for prognosticators, who can only contribute one successful prediction throughout the entirety of their careers. After achieving such, they remain a trusted source, with all of their previous crack-pot predictions washed away. 

Yet despite what I have just described, the madness of this charade continues. 

Is it just for the fun of it all? The belief that through ritualization, the impossible could potentially become possible? Or maybe it's just the human need to create experts.

Whatever the case may be, I refuse to consider these male astrology exercises to be anything more than the board room equivalent of camp fire stories.

The Data

# S&P 500 Total Returns by Year (Percent change) #

# https://www.slickcharts.com/sp500/returns #

sp_close_72_22 <- c(-18.11, 28.71, 18.4, 31.49, -4.38, 21.83, 11.96, 1.38, 13.69, 32.39, 16, 2.11, 15.06, 26.46, -37, 5.49, 15.79, 4.91, 10.88, 28.68, -22.1, -11.89, -9.1, 21.04, 28.58, 33.36, 22.96, 37.58, 1.32, 10.08, 7.62, 30.47, -3.1, 31.69, 16.61, 5.25, 18.67, 31.73, 6.27, 22.56, 21.55, -4.91, 32.42, 18.44, 6.56, -7.18, 23.84, 37.2, -26.47, -14.66, 18.98)


# CPI Percentage Change Dec-Dec #

# https://www.usinflationcalculator.com/inflation/consumer-price-index-and-annual-percent-changes-from-1913-to-2008/ #

cpi_72_22 <- c(6.5, 7, 1.4, 2.3, 1.9, 2.1, 2.1, 0.7, 0.8, 1.5, 1.7, 3, 1.5, 2.7, 0.1, 4.1, 2.5, 3.4, 3.3, 1.9, 2.4, 1.6, 3.4, 2.7, 1.6, 1.7, 3.3, 2.5, 2.7, 2.7, 2.9, 3.1, 6.1, 4.6, 4.4, 4.4, 1.1, 3.8, 3.9, 3.8, 3.8, 8.9, 12.5, 13.3, 9, 6.7, 4.9, 6.9, 12.3, 8.7, 3.4)


# 30-year fixed-rate average #

# https://www.bankrate.com/mortgages/historical-mortgage-rates/#current-rates #

thirty_year_mor_72_22 <- c(0.0553, 0.0315, 0.0338, 0.0413, 0.047, 0.0414, 0.0379, 0.0399, 0.0431, 0.0416, 0.0388, 0.0465, 0.0486, 0.0538, 0.0623, 0.064, 0.0647, 0.0593, 0.0588, 0.0589, 0.0657, 0.0701, 0.0808, 0.0746, 0.0691, 0.0757, 0.0776, 0.0786, 0.0828, 0.0717, 0.0827, 0.0909, 0.0997, 0.1025, 0.1038, 0.104, 0.1039, 0.1243, 0.1388, 0.1324, 0.1604, 0.1664, 0.1374, 0.112, 0.0964, 0.0885, 0.0887, 0.0905, 0.0919, 0.0804, 0.0738)


# M2 Percent Change from Year Ago #

# https://fred.stlouisfed.org/graph/?graph_id=248494 #

m2_72_22 <- c(5.11903, 16.28949, 19.11447, 5.06449, 3.77566, 5.68219, 6.76589, 5.76268, 6.167, 6.73845, 8.57838, 7.30235, 2.49613, 8.02493, 6.75141, 6.11739, 5.23708, 4.28224, 4.7706, 6.97704, 7.44801, 8.63346, 6.04183, 7.38864, 7.15112, 5.27695, 4.8759, 2.07367, 1.26729, 1.03366, 1.86908, 3.71999, 5.50776, 4.19323, 5.35027, 6.48672, 8.12228, 8.90245, 8.00654, 12.20922, 9.0296, 9.03193, 8.0325, 7.82262, 8.27402, 12.39339, 12.76942, 9.41921, 5.86709, 9.70773, 12.41968)

The Sources

“S&P 500 Total Returns.” S&P 500 Total Returns by Year Since 1926,                    www.slickcharts.com/sp500/returns. Accessed 5 Nov. 2023.

“Consumer Price Index Data from 1913 to 2023.” US Inflation Calculator | Easily Calculate How the Buying Power of the U.S. Dollar Has Changed from 1913 to 2023. Get Inflation Rates and U.S. Inflation News., 12 Oct. 2023, www.usinflationcalculator.com/inflation/consumer-price-index-and-annual-percent-changes-from-1913-to-2008.

“M2.” FRED, fred.stlouisfed.org/graph/?graph_id=248494. Accessed 5 Nov. 2023.

The Analysis

###########################################################################

# Getting the Libraries in Order #

library("ggpubr")

library(tseries)

###########################################################################

cor.test(sp_close_72_22, cpi_72_22)

cor.test(sp_close_72_22, thirty_year_mor_72_22)

cor.test(sp_close_72_22, m2_72_22)

cor.test(cpi_72_22, m2_72_22)

###########################################################################

# Visual Creation Output #

###########################################################################

my_data <- data.frame(sp_close_72_22, cpi_72_22)

ggscatter(my_data, x = "sp_close_72_22", y = "cpi_72_22",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "S&P 500 Total Returns by Year (Percent change)", ylab = "CPI Percent Change Dec-Dec")



my_data <- data.frame(sp_close_72_22, thirty_year_mor_72_22)

ggscatter(my_data, x = "sp_close_72_22", y = "thirty_year_mor_72_22",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "S&P 500 Total Returns by Year (Percent change)", ylab = "30-year fixed-rate average")


my_data <- data.frame(sp_close_72_22, m2_72_22)

ggscatter(my_data, x = "sp_close_72_22", y = "m2_72_22",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "S&P 500 Total Returns by Year (Percent change)", ylab = "M2 Percent Change from Year Ago")


my_data <- data.frame(m2_72_22, cpi_72_22)

ggscatter(my_data, x = "m2_72_22", y = "cpi_72_22",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "M2 Percent Change from Year Ago", ylab = "CPI Percent Change Dec-Dec")

###########################################################################

Findings

There was a negative correlation between the two variables: S&P 500 Total Returns by Year (Percent change) (n = 51) and CPI Percent Change Dec-Dec (n = 51). S&P 500 Total Returns by Year (M = 11.983, SD = 17.536), CPI Percent Change Dec-Dec (M = 3.992, SD = 3.032), Conditions; t(49) = -0.82177, p = .42. Pearson Product-Moment Correlation Coefficient: r = -.12.

There was a positive correlation between the two variables: S&P 500 Total Returns by Year (Percent change) (n = 51) and 30-year fixed-rate average (n = 51). S&P 500 Total Returns by Year (Percent change) (M = 11.983, SD = 17.536), 30-year fixed-rate average (M = .078, SD = .032), Conditions; t(49) = 0.29162, p = .77. Pearson Product-Moment Correlation Coefficient: r = .04.

There was a positive correlation between the two variables: S&P 500 Total Returns by Year (Percent change) (n = 51) and M2 Percent Change from Year Ago (n = 51). S&P 500 Total Returns by Year (Percent change) (M = 11.983, SD = 17.536), M2 Percent Change from Year Ago (M = 7.085, SD = 3.464), Conditions; t(49) = 0.58362, p = .56. Pearson Product-Moment Correlation Coefficient: r = .08.

There was a positive correlation between the two variables: CPI Percent Change Dec-Dec (n = 51) and M2 Percent Change from Year Ago (n = 51). CPI Percent Change Dec-Dec (M = 3.992, SD = 3.032), M2 Percent Change from Year Ago (M = 7.085, SD = 3.464), Conditions; t(49) = 1.4331, p = .16. Pearson Product-Moment Correlation Coefficient: r = .20. 

Conclusions

As is evident from our findings, there is not a single economic indicator which demonstrates a 1:1 correlation of any significance (alpha = .05). Therefore, we can infer that news headlines which contains hyperbolic language such as:

The Jobs Market Is A Recession Warning

Major U.S. indicators point to a recession starting

XYZ strategist sees year-end equities rally

Economic Indicator Says Recession Imminent

Are ultimately the work of some vaudeville spirit medium summoning imaginary ghosts to a drawing room.

The closest that we came to discerning anything of interest, was the non-significant (p = .16), but still somewhat insightful, correlative (r = .20) assessment of CPI and M2. The impact of money supply on CPI figures should be somewhat self-evident. However, with the coefficient of determination being less than .50, we can only make the assessment that the increase of currency within a financial system might increase the rate of inflation. Sometimes, but not always.

All these revelations should shine a light in the darkness as it pertains to the definitive pronouncements of various opaque economic models. Almost as if by design, the failure of such doomsday warnings are rarely revisited the day after our purported judgement. However, this does little to inhibit the same modeling systems from being trotted out time and again.

Once a system has been established, all the evidence which is contra to its continued existence is explained away in terms of circumstance, with no fault being assigned to the system itself. The same holds true for reputations, and un-verified phenomenon.

I read somewhere that the ancient Greeks assessed their heroes not upon their fates, but as to how those heroes behaved within heroic situations. The qualities of temperance and mastery of the self, were what ultimately determined the differentiating attributes of heroism. Perhaps the modern world can learn something from this perspective. That honest action within itself, regardless of the outcome, is that which ultimately provides the truth.

-RD

(R) Does Trading Volume Impact Stock Index Pricing?

In a previous article, we concluded that US equity markets are random. At least that is what was determined based upon our research. I was willing to mark this matter as being solved, however, prior to doing such, a reader of this site sent a message inquiring about the Winner’s Curse, and how this phenomenon might be applied to stock pricing. 

Disproving the Winner’s Curse

The winner's curse is a phenomenon that may occur in common value auctions, where all bidders have the same (ex post) value for an item but receive different private (ex ante) signals about this value and wherein the winner is the bidder with the most optimistic evaluation of the asset and therefore will tend to overestimate and overpay.

“Winner’s Curse.” Wikipedia, Wikimedia Foundation, 17 Oct. 2023,         en.wikipedia.org/wiki/Winner%27s_curse.

In plain terms, this basically states that the number of bids within an auction, ought to drive up the price of the item being sold. Let’s take a look at this phenomenon as it is applied to the stock market. After all, one probably should expect to observe such a phenomenon within this medium.

To perform the appropriate analysis, I gathered the monthly closing percentage figures for three different stock indices (S&P 500, Nikkei 225, STOXX 600). The months included within this study are November 2003 – September 2023. Data was queried from Yahoo Finance.

I will be utilizing the Pearson's product-moment correlation to test for relationships as it pertains to the index volume for each month, as assessed in comparison to the percentage differentiation of closing price.

I will also test for randomness as it pertains to monthly volume figures through the utilization of the Phillips-Perron Unit Root Test.

Finally, I will test for stationarity amongst monthly volume figures through the application of the Augmented Dicky-Fuller methodology.

###########################################################################

# Getting the Libraries in Order #

library("ggpubr")

library(tseries)

###########################################################################

# S&P 500 (USA) #

###########################################################################

sp_close <- c(0.007, 0.051, 0.017, 0.012, -0.016, -0.017, 0.012, 0.018, -0.034, 0.002, 0.009, 0.014, 0.039, 0.032, -0.025, 0.019, -0.019, -0.02, 0.03, 0, 0.036, -0.011, 0.007, -0.018, 0.035, -0.001, 0.025, 0, 0.011, 0.006, -0.031, 0, 0.005, 0.02, 0.025, 0.032, 0.017, 0.013, 0.014, -0.022, 0.01, 0.043, 0.033, -0.018, -0.033, 0.013, 0.036, 0.014, -0.042, -0.008, -0.061, -0.035, -0.006, 0.045, 0.01, -0.085, -0.007, 0.011, -0.094, -0.168, -0.075, 0.016, -0.085, -0.107, 0.094, 0.1, 0.053, -0.004, 0.072, 0.031, 0.037, -0.018, 0.057, 0.015, -0.038, 0.028, 0.058, 0.013, -0.083, -0.052, 0.068, -0.053, 0.087, 0.035, -0.004, 0.06, 0.023, 0.03, -0.002, 0.026, -0.015, -0.018, -0.021, -0.057, -0.072, 0.108, -0.003, 0.009, 0.043, 0.041, 0.031, -0.007, -0.063, 0.04, 0.012, 0.02, 0.024, -0.02, 0.003, 0.007, 0.05, 0.011, 0.036, 0.018, 0.021, -0.016, 0.047, -0.033, 0.028, 0.044, 0.027, 0.023, -0.034, 0.043, 0.008, 0.005, 0.021, 0.019, -0.016, 0.038, -0.016, 0.024, 0.024, -0.003, -0.031, 0.054, -0.018, 0.009, 0.01, -0.022, 0.018, -0.063, -0.025, 0.083, 0, -0.019, -0.048, -0.002, 0.063, 0.004, 0.014, 0.002, 0.035, -0.001, -0.001, -0.018, 0.033, 0.018, 0.012, 0.034, -0.007, 0.009, 0.01, 0.003, 0.016, -0.002, 0.018, 0.021, 0.025, 0.011, 0.052, -0.036, -0.027, 0.006, 0.024, 0, 0.041, 0.028, 0.006, -0.073, 0.016, -0.102, 0.092, 0.03, 0.013, 0.034, -0.068, 0.069, 0.003, -0.018, 0.023, 0.018, 0.03, 0.028, -0.006, -0.087, -0.131, 0.166, 0.061, 0.02, 0.053, 0.064, -0.041, -0.034, 0.099, 0.03, -0.013, 0.021, 0.034, 0.047, 0.003, 0.019, 0.022, 0.026, -0.049, 0.067, -0.009, 0.035, -0.055, -0.032, 0.038, -0.09, 0, -0.088, 0.092, -0.038, -0.089, 0.073, 0.046, -0.061, 0.058, -0.025, 0.037, 0.016, 0.003, 0.064, 0.031, -0.016, -0.054)

sp_vol <- c(24463220000, 27839130000, 32820000000, 27985600000, 33597900000, 31611900000, 29326400000, 27529500000, 29285600000, 26586800000, 26829870000, 31511000000, 30460280000, 31102500000, 31498800000, 29297410000, 39014150000, 43424270000, 39321990000, 40334040000, 37464670000, 42030090000, 44777510000, 49793790000, 45102870000, 41756130000, 49211650000, 42859940000, 50905040000, 43308430000, 54312830000, 54873260000, 46348220000, 50485620000, 49001440000, 56793620000, 55343930000, 47578780000, 56686200000, 51844990000, 67622250000, 57032470000, 64958050000, 65322800000, 70337430000, 91381760000, 57809700000, 76022580000, 86246950000, 64821670000, 98475340000, 78536130000, 93189170000, 85978630000, 80990480000, 96614040000, 124980570000, 86266010000, 140007320000, 159823030000, 115660210000, 112884470000, 112090640000, 124492210000, 161843640000, 138855320000, 131614940000, 112653150000, 106635790000, 116059270000, 112295490000, 113410990000, 84981530000, 89515330000, 90947580000, 84561340000, 103683550000, 116741910000, 127662780000, 110106750000, 94778110000, 85738250000, 79589450000, 89536270000, 87151070000, 80984530000, 92164940000, 59223660000, 89507640000, 77364810000, 81708980000, 86122730000, 81102170000, 108419170000, 102786820000, 98063670000, 84275050000, 74742430000, 79567560000, 78385710000, 83899660000, 74761710000, 86920490000, 81582440000, 73103810000, 70283810000, 69784280000, 71752320000, 71489310000, 66388180000, 75848510000, 69273480000, 68527110000, 77098000000, 76447250000, 74946790000, 68106820000, 64802810000, 66174410000, 76647400000, 63628190000, 64958820000, 75871910000, 69725590000, 71885030000, 71595810000, 63623630000, 63283380000, 66524690000, 58131140000, 66706000000, 93714040000, 63600190000, 80743820000, 77330040000, 68775560000, 76675850000, 72060940000, 65187730000, 73213980000, 77920590000, 84626790000, 79989370000, 85844900000, 75943590000, 83649260000, 92409770000, 93049560000, 92639420000, 81124990000, 78883600000, 86852700000, 69530250000, 75610310000, 77023620000, 72915530000, 88445380000, 75344550000, 70576420000, 69260940000, 81664010000, 65369860000, 79719460000, 81078810000, 63348090000, 70784900000, 66624120000, 71088550000, 73416960000, 65531700000, 77318690000, 79933970000, 76803890000, 70194700000, 76011820000, 77891360000, 64898300000, 69523070000, 63031510000, 91930980000, 80620020000, 84162180000, 80859870000, 70638770000, 79159660000, 70090370000, 77250740000, 71250630000, 70599470000, 80269220000, 74178980000, 77720640000, 72410620000, 72325540000, 77287980000, 84436590000, 162185380000, 123608160000, 107135190000, 131458880000, 96928130000, 82466520000, 92310780000, 89938980000, 101247180000, 96375680000, 106117800000, 99082320000, 122371150000, 83124090000, 88321860000, 102544180000, 84255620000, 80500760000, 85528860000, 80253600000, 88268840000, 92750180000, 95562890000, 92667710000, 123546260000, 90367840000, 108860390000, 106116710000, 81688320000, 92252350000, 94241020000, 95823760000, 92671910000, 85249330000, 80763810000, 80392280000, 113094800000, 70861260000, 88929200000, 87983140000, 75063200000, 86840820000, 73482980000)

cor.test(sp_close, sp_vol)

PP.test(sp_vol)

adf.test(sp_vol)

###########################################################################

# Nikkei 225 (JAPAN) #

###########################################################################

nik_vol <- c(2103300000, 1973300000, 1923900000, 2093700000, 1779800000, 1305200000, 1782200000, 1369700000, 1364600000, 1484200000, 1555800000, 1435500000, 1377200000, 1397800000, 1339300000, 1637700000, 1582900000, 1345900000, 1882500000, 1390900000, 1387900000, 1284100000, 1433700000, 1601900000, 1561500000, 1235400000, 1108100000, 1258700000, 1313600000, 1231300000, 1956500000, 1406000000, 1388600000, 1340300000, 1614800000, 1148600000, 1362400000, 1357300000, 1454700000, 1754000000, 1539400000, 1837200000, 3101700000, 1396200000, 1133600000, 1173000000, 1356700000, 1347900000, 1392600000, 1373500000, 1168700000, 1195400000, 1458100000, 1187800000, 1396900000, 1276100000, 1275600000, 1529200000, 1534700000, 1822800000, 1447600000, 1515200000, 1523800000, 1513500000, 1607600000, 1386000000, 1732700000, 1840200000, 1606300000, 1539000000, 1981200000, 1872800000, 1807500000, 1876000000, 1790600000, 2326500000, 2230200000, 2178500000, 2646000000, 2606300000, 2440400000, 3038700000, 3226000000, 2222800000, 2493200000, 2675600000, 2816900000, 3093000000, 2563800000, 3230600000, 3307500000, 4174100000, 3235900000, 2749100000, 2559500000, 2979600000, 3132300000, 3723100000, 3318200000, 3459500000, 3291500000, 3047400000, 3191800000, 2975400000, 2691500000, 2962900000, 3155400000, 3436700000, 2530100000, 2300800000, 2467400000, 2715300000, 2560200000, 2575500000, 3011800000, 3390300000, 3734900000, 3151000000, 3175900000, 3095600000, 2908600000, 3158800000, 4145700000, 4755100000, 7190600000, 6211600000, 4251700000, 5299900000, 4335800000, 3432700000, 2687500000, 2738800000, 2403400000, 2571500000, 2457400000, 2548800000, 2713200000, 2547300000, 3340600000, 3455900000, 2153800000, 2086100000, 2276100000, 2371900000, 2664200000, 3428500000, 2450800000, 2889600000, 2475600000, 2991400000, 4792200000, 3125000000, 2736000000, 2638500000, 2736400000, 2922000000, 2480200000, 2551700000, 2938300000, 2699700000, 3169300000, 3039100000, 2840200000, 2486300000, 3461300000, 3335300000, 2760300000, 3133500000, 2585200000, 2927600000, 3393000000, 3795800000, 3006700000, 3798500000, 3376900000, 2809500000, 2655200000, 2663800000, 2850200000, 4267300000, 2905700000, 2443300000, 2658600000, 2825900000, 2699700000, 2572700000, 2821400000, 2916400000, 3114100000, 2330800000, 3089900000, 2633300000, 2068700000, 3199300000, 2635500000, 2726700000, 2759200000, 2597500000, 3402500000, 3256500000, 2668700000, 2415700000, 2143600000, 2207200000, 2062500000, 2278400000, 2085700000, 2526300000, 2337600000, 2145500000, 2389600000, 2767300000, 2680600000, 3239400000, 3468100000, 3283900000, 3272000000, 2344500000, 1432300000, 1617600000, 1446100000, 1675000000, 2032200000, 1665700000, 1616200000, 1437800000, 1400600000, 1588400000, 1666700000, 1481800000, 1373300000, 1704500000, 1696200000, 2430200000, 2429300000, 1282100000, 1436200000, 1274000000, 1273100000)

nik_close <- c(-0.021, -0.021, -0.01, 0.069, 0.059, 0.023, 0.024, -0.001, 0.055, -0.083, 0.013, 0.066, -0.072, 0.01, 0.048, -0.034, 0.016, -0.029, 0.035, -0.024, -0.078, 0.032, -0.054, -0.012, 0.043, 0.021, -0.057, -0.007, -0.006, -0.022, -0.008, 0.045, 0.003, 0.03, 0.126, -0.009, 0.004, 0.052, -0.029, 0.017, 0.086, 0.075, -0.102, -0.082, -0.005, 0.011, 0.024, 0.048, 0.052, -0.032, -0.002, 0.045, -0.077, 0.034, -0.013, 0.028, 0.054, -0.131, 0.02, -0.103, 0.054, 0.01, 0.014, 0.008, -0.011, 0.046, -0.021, -0.055, 0.001, -0.007, 0.026, 0.073, 0.031, -0.013, -0.007, 0.017, 0.025, 0.011, -0.017, 0.01, -0.014, 0.03, 0.051, 0.049, -0.026, 0.028, 0.053, -0.098, 0.051, -0.003, 0.044, -0.104, -0.074, -0.04, 0.047, 0.084, -0.079, -0.087, 0.014, -0.01, 0.051, 0.02, 0.018, 0.067, 0.02, -0.001, 0.042, 0.015, 0.044, -0.006, 0.028, 0.025, 0.02, -0.04, 0.011, 0.004, -0.083, 0.039, 0.08, -0.013, 0.07, -0.021, -0.006, 0.009, -0.005, 0.107, 0.075, 0.032, 0.048, 0.088, 0.054, 0.013, 0.004, 0.025, -0.047, 0.06, -0.109, -0.067, 0.031, 0.096, 0.029, -0.015, -0.053, 0.047, -0.036, -0.106, -0.005, 0.011, -0.028, 0.009, -0.094, 0.032, -0.011, 0.028, 0.078, -0.026, 0.057, -0.085, 0.025, -0.039, -0.11, -0.011, 0.087, -0.009, -0.04, 0.12, -0.06, -0.004, -0.032, 0.013, 0.045, 0.044, 0.071, 0.074, 0.081, -0.045, -0.125, 0.045, -0.022, -0.329, -0.149, -0.016, -0.01, -0.064, 0.037, 0.095, -0.071, 0.006, -0.115, -0.029, -0.072, -0.002, 0.016, -0.036, -0.052, 0.01, 0.027, 0.003, -0.015, 0.013, 0.004, 0.053, -0.004, 0.014, 0.003, 0.047, -0.008, -0.006, -0.095, -0.013, 0.061, -0.024, 0.021, 0.074, 0.078, 0.003, 0.079, 0.041, 0.027, 0.031, 0.029, -0.053, -0.006, 0.027, -0.006, 0.061, 0.015, -0.011, -0.026, -0.017, -0.054, 0.055, -0.048, 0, 0.051, 0.023, 0, 0.063, -0.059)

cor.test(nik_close, nik_vol)

PP.test(nik_vol)

adf.test(stoxx_vol)

###########################################################################

# STOXX 600 (EUROPE) #

###########################################################################

stoxx_vol <- c(2082064000, 3593140000, 3623085900, 3227490000, 3963845100, 4537933600, 3364175000, 5644136700, 4315542500, 4190288900, 3429359000, 4428634700, 4324893100, 5044459900, 3673166200, 4209030900, 4403288200, 4668497000, 4080039400, 7015693000, 4665939400, 4219964500, 3725329800, 5141114500, 3873973500, 3990773300, 3214970700, 3353233300, 3727672100, 3913126100, 3529714100, 4851670900, 4375370400, 4120573200, 4414589500, 5990354800, 4457050500, 4378642700, 3472143000, 4493206100, 6506693200, 5685330700, 5778662500, 9781539200, 4717665900, 3747876800, 3687903800, 3914857000, 4634906100, 4167228400, 4371274100, 3994185300, 3822333900, 4370401300, 3655958900, 4272524500, 3844484400, 3935024300, 4010016100, 4369953900, 4636643000, 3756703600, 3675091700, 3686458400, 4898417700, 5329248500, 4001420700, 4761109700, 4563697300, 4414670700, 3765308000, 4558362700, 4396511200, 3962271900, 3806938800, 4136701600, 5288574400, 5776592600, 4559447300, 5731696800, 4727016300, 5108929600, 5481488800, 6189735400, 5284539900, 5715861400, 5162109900, 6441906800, 8798906100, 5814206300, 6047662900, 6569684600, 7243086800, 6170797300, 4829569500, 5156214200, 5810022700, 5920225300, 5598217400, 5667279400, 6016609900, 5530892100, 5447295400, 6784088400, 6455256800, 7130308000, 5601864000, 5783571900, 8068259800, 5715514200, 5061411200, 6041303100, 5109740500, 5664157800, 6260120300, 7557556000, 5391112100, 6532452900, 4626036900, 5155068400, 6300416000, 5596521600, 5120640200, 459936200)

stoxx_close <- c(-0.002, -0.018, -0.028, 0.02, 0.021, -0.034, 0.019, -0.006, 0.016, 0.06, -0.039, 0.061, 0.063, -0.069, -0.054, 0.074, -0.089, -0.011, -0.013, 0.006, -0.038, -0.041, 0.049, -0.028, 0.05, -0.037, 0.018, 0.018, 0.012, 0.02, 0.018, 0.05, 0.02, -0.012, 0.023, 0.119, -0.057, -0.017, 0.028, -0.013, 0.024, 0.033, 0.07, -0.183, -0.094, -0.014, 0.02, 0.025, 0.009, 0.034, -0.014, 0.001, 0.042, -0.061, 0.03, 0.015, 0.037, 0.064, -0.065, -0.012, -0.06, 0.003, -0.025, 0.033, -0.009, -0.006, 0.041, -0.021, -0.044, 0.016, 0.006, -0.024, 0.017, 0.035, -0.012, -0.006, -0.027, 0.008, 0.013, 0.025, 0.024, -0.003, 0.053, 0.006, -0.009, -0.004, 0.003, 0.033, -0.052, 0.017, 0.016, 0.011, -0.029, -0.068, -0.056, 0.029, 0.069, -0.035, -0.095, 0.034, -0.052, 0.012, -0.002, 0.014, 0.064, 0.063, -0.009, 0.03, -0.018, 0.002, 0.018, -0.019, -0.008, 0.019, 0.009, -0.005, 0.047, -0.02, 0.008, 0.008, 0.036, 0.037, -0.01, 0.043)

cor.test(stoxx_close, stoxx_vol)

PP.test(stoxx_vol)

adf.test(stoxx_vol)

###########################################################################

# Visual Creation Output #

###########################################################################

# S&P 500 (USA) #

my_data <- data.frame(sp_close, sp_vol)


ggscatter(my_data, x = "sp_vol", y = "sp_close",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "S&P 500 Monthly Volume", ylab = "S&P 500 Monthly Close")


# Nikkei 225 (JAPAN) #

my_data <- data.frame(nik_close, nik_vol)


ggscatter(my_data, x = "nik_vol", y = "nik_close",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "Nikkei 225 Monthly Volume", ylab = "Nikkei 225 Monthly Close")


# STOXX 600 (EUROPE) #

my_data <- data.frame(stoxx_close, stoxx_vol)


ggscatter(my_data, x = "stoxx_vol", y = "stoxx_close",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "STOXX 600 Monthly Volume", ylab = "STOXX 600 Monthly Close")

###########################################################################

Initial Findings

There was a negative correlation between the two variables: S&P 500 Monthly Close (n = 239) and S&P 500 Monthly Volume (n = 239). S&P 500 Monthly Close (M = .006, SD = .043), S&P 500 Monthly Volume (M = 77899674812, SD = 24642426931), Conditions; t(237) = -2.1245, p = .03. Pearson Product-Moment Correlation Coefficient: r = -.14.

There was a negative correlation between the two variables: Nikkei 225 Monthly Close (n = 239) and Nikkei 225 Monthly Volume (n = 239). Nikkei 225 Monthly Close (M = .003, SD = .055), Nikkei 225 Monthly Volume (M = 2400008787, SD = 912823479), Conditions; t(237) = -0.48111, p = .63. Pearson Product-Moment Correlation Coefficient: r = -.03.

There was a negative correlation between the two variables: STOXX 600 Monthly Close (n = 124)* and STOXX 600 Monthly Volume (n = 124). STOXX 600 Monthly Close (M = .002, SD = .041), STOXX 600 Monthly Volume (M = 4885890780, SD = 1260418703), Conditions; t(122) = -2.0375, p = .04. Pearson Product-Moment Correlation Coefficient: r = -.18.

* - Only limited historical data was available for the STOXX 600 index.

Initial Conclusions

The results of this analysis indicates that there is a correlative relationship as it pertains to volume and closing price; at least, as it pertains to the S&P 500 and the STOXX 600. These indexes are of American, and European origin, respectively. However, this phenomenon was not evident in the results of the analysis as it pertains to the Nikkei 225, a Japanese stock market index. There is an old adage in the field of economics, which is typically some variation of: treat the Japanese economy as a singular non-universalized phenomenon, in which, observations related to such cannot be applied to other instances within the field as whole. This truism seems to hold merit as it relates to these findings. 

Interestingly, each analytical outcome demonstrates a weak modeling potential. The Pearson Product-Moment Correlation Coefficient as it pertains to each index is negative, with the Japanese Nikkei 225 possessing the lowest coefficient figure: - .03.

This would seemingly indicate the inverse conclusion inferred by, “The Winner’s Curse”. 

As is observed within the above graphics, the volume which exists within each market, appears to drive down market pricing. Even if the effect is marginal and inconsistent, it exists nevertheless.

Though this really ought to fly in the face of fundamental economic theory, we must ask ourselves, does it really? According to Say’s Law, supply creates its own demand. Therefore, would it stand to reason that the inverse ought to be true? Does demand create its own supply?

Additional Research

With this in mind, I decided to perform some additional analysis in order to either support or disprove the initial findings.

Utilizing my favorite outlier function, I searched for potential outlier values within the volume variables for each individual index. 

OutlierFunction <- function(t){

q1 <- fivenum(t)

q1 <- q1[2] #Q1

q3 <- fivenum(t)

q3 <- q3[4] #Q3

iqrange <- q3 - q1

out1 <<- (q1 - (iqrange * 1.5))

out2 <<- (q3 + (iqrange * 1.5))

lowout <<- subset(t, t < out1, na.rm = TRUE)

highout <<- subset(t, t > out2, na.rm = TRUE)

}

OutlierFunction()

This turned up the following values as it pertains to each index.

S&P 500 – 124980570000, 140007320000, 159823030000, 124492210000, 161843640000, 138855320000, 131614940000, 127662780000, 162185380000, 131458880000, 24463220000, 27839130000, 27985600000, 29326400000, 27529500000, 29285600000, 26586800000, 26829870000, 30460280000, 31102500000, 29297410000

Nikkei 225 – 7190600000, 6211600000, 5299900000

STOXX 600 – 9781539200, 8798906100, 459936200

I then matched these volume values to their corresponding closing figures.

S&P 500 

Nikkei 225

STOXX 600

Next, I ran additional analysis on the data vectors with outlier values removed.

###########################################################################

# S&P 500 (USA) OUTLIERS! #

###########################################################################

sp_close <- c(0.166, 0.038, 0.034, 0.013, 0.031, -0.075, -0.018, 0.037, 0.016, -0.004, 0.037, -0.085, -0.052, 0, -0.057, 0.061, 0.072, -0.013, -0.088, 0.058, -0.072, 0.019, 0.099, 0.021, -0.061, 0.108, 0.053, -0.085, 0.03, 0.073, -0.055, 0.068, -0.089, 0.024, -0.006, -0.002, 0.035, 0.046, -0.032, 0.063, -0.048, -0.041, -0.038, 0.023, -0.073, 0.013, -0.038, -0.09, -0.034, 0.035, 0.015, -0.002, 0.003, 0.033, 0.003, -0.009, 0.064, -0.004, -0.063, 0.002, -0.016, 0.011, -0.042, -0.018, 0.045, 0.083, -0.053, -0.049, -0.061, 0.057, -0.063, 0.028, -0.087, -0.003, 0.022, -0.102, 0.031, -0.019, 0.047, 0.064, -0.015, 0.092, -0.007, 0.04, 0.004, -0.021, 0.003, 0.01, 0.06, 0.092, 0.058, -0.003, 0.016, 0.026, -0.025, -0.018, 0.067, -0.025, -0.036, 0.01, 0.087, 0.043, 0.013, 0.014, -0.035, 0.041, 0.018, 0, 0.018, 0.026, -0.031, 0.052, -0.006, -0.068, 0.018, -0.001, -0.027, -0.018, 0.044, 0.021, 0.014, 0.024, 0, -0.034, 0.05, -0.001, 0.018, 0.031, -0.016, -0.007, 0.009, 0.023, -0.054, 0.025, -0.022, 0.012, -0.018, 0.03, 0.028, 0.009, 0.008, -0.02, 0.005, 0.003, 0.069, 0.021, 0.016, -0.002, 0.03, 0.003, 0.012, -0.033, 0.02, 0.006, 0.034, 0.024, 0.043, 0.035, 0.028, 0.011, 0.034, 0.054, 0.036, 0.047, 0.01, -0.016, 0.018, -0.016, 0.007, 0.028, 0.011, 0.009, -0.018, 0.01, 0.023, 0.033, 0.041, -0.008, -0.033, 0.027, 0.021, 0.024, 0.016, 0.019, 0.006, 0.03, 0.038, 0.036, 0.043, 0.032, 0.014, 0.017, 0, -0.031, -0.022, 0.011, 0.02, -0.018, 0.025, 0.025, 0.013, 0.005, 0.035, 0.007, -0.02, 0.006, 0, -0.011, -0.001, 0, 0.03, -0.019, 0.036, -0.016, 0.017, -0.017, 0.014, -0.025)

sp_vol <- c(123608160000, 123546260000, 122371150000, 116741910000, 116059270000, 115660210000, 113410990000, 113094800000, 112884470000, 112653150000, 112295490000, 112090640000, 110106750000, 108860390000, 108419170000, 107135190000, 106635790000, 106117800000, 106116710000, 103683550000, 102786820000, 102544180000, 101247180000, 99082320000, 98475340000, 98063670000, 96928130000, 96614040000, 96375680000, 95823760000, 95562890000, 94778110000, 94241020000, 93714040000, 93189170000, 93049560000, 92750180000, 92671910000, 92667710000, 92639420000, 92409770000, 92310780000, 92252350000, 92164940000, 91930980000, 91381760000, 90947580000, 90367840000, 89938980000, 89536270000, 89515330000, 89507640000, 88929200000, 88445380000, 88321860000, 88268840000, 87983140000, 87151070000, 86920490000, 86852700000, 86840820000, 86266010000, 86246950000, 86122730000, 85978630000, 85844900000, 85738250000, 85528860000, 85249330000, 84981530000, 84626790000, 84561340000, 84436590000, 84275050000, 84255620000, 84162180000, 83899660000, 83649260000, 83124090000, 82466520000, 81708980000, 81688320000, 81664010000, 81582440000, 81124990000, 81102170000, 81078810000, 80990480000, 80984530000, 80859870000, 80763810000, 80743820000, 80620020000, 80500760000, 80392280000, 80269220000, 80253600000, 79989370000, 79933970000, 79719460000, 79589450000, 79567560000, 79159660000, 78883600000, 78536130000, 78385710000, 77920590000, 77891360000, 77720640000, 77364810000, 77330040000, 77318690000, 77287980000, 77250740000, 77098000000, 77023620000, 76803890000, 76675850000, 76647400000, 76447250000, 76022580000, 76011820000, 75943590000, 75871910000, 75848510000, 75610310000, 75344550000, 75063200000, 74946790000, 74761710000, 74742430000, 74178980000, 73482980000, 73416960000, 73213980000, 73103810000, 72915530000, 72410620000, 72325540000, 72060940000, 71885030000, 71752320000, 71595810000, 71489310000, 71250630000, 71088550000, 70861260000, 70784900000, 70638770000, 70599470000, 70576420000, 70337430000, 70283810000, 70194700000, 70090370000, 69784280000, 69725590000, 69530250000, 69523070000, 69273480000, 69260940000, 68775560000, 68527110000, 68106820000, 67622250000, 66706000000, 66624120000, 66524690000, 66388180000, 66174410000, 65531700000, 65369860000, 65322800000, 65187730000, 64958820000, 64958050000, 64898300000, 64821670000, 64802810000, 63628190000, 63623630000, 63600190000, 63348090000, 63283380000, 63031510000, 59223660000, 58131140000, 57809700000, 57032470000, 56793620000, 56686200000, 55343930000, 54873260000, 54312830000, 51844990000, 50905040000, 50485620000, 49793790000, 49211650000, 49001440000, 47578780000, 46348220000, 45102870000, 44777510000, 43424270000, 43308430000, 42859940000, 42030090000, 41756130000, 40334040000, 39321990000, 39014150000, 37464670000, 33597900000, 32820000000, 31611900000, 31511000000, 31498800000)

cor.test(sp_close, sp_vol)

###########################################################################

# Nikkei 225 (JAPAN) OUTLIERS! #

###########################################################################

nik_vol <- c(-0.094, 0.009, 0.048, -0.329, 0.075, -0.104, -0.006, 0.074, 0.044, -0.083, -0.087, 0.078, -0.04, -0.01, 0.096, 0.015, 0.088, -0.106, -0.015, 0.045, 0.004, 0.081, 0.031, 0.12, 0.014, 0.044, 0.051, 0.003, 0.079, 0.013, 0.074, -0.074, -0.003, 0.051, -0.036, 0.018, 0.08, -0.11, -0.021, 0.042, 0.039, -0.004, -0.079, 0.032, -0.115, -0.102, -0.013, -0.098, -0.072, 0.02, -0.011, 0.03, 0.011, 0.071, 0.009, 0.084, 0.067, -0.001, 0.025, 0.013, -0.026, 0.006, 0.07, -0.149, 0.011, -0.022, 0.087, -0.064, -0.071, 0.053, -0.045, -0.024, -0.06, 0.027, -0.04, 0.013, 0.078, -0.011, 0.01, 0.025, -0.109, -0.039, 0.037, 0.02, 0.054, 0.021, 0.028, 0.004, -0.036, 0.045, -0.01, -0.125, -0.017, 0.028, -0.052, -0.002, 0.01, 0.003, -0.032, -0.04, 0.095, 0.025, 0.051, 0.02, 0.047, -0.085, 0.06, -0.067, 0.044, -0.006, -0.026, -0.009, 0.057, -0.028, 0.028, -0.047, -0.005, -0.016, -0.014, 0, 0.051, 0.053, 0.004, 0.061, 0.047, 0.041, -0.095, -0.029, 0.017, -0.006, 0.047, -0.053, 0.025, 0.049, 0.014, 0.011, 0.029, -0.013, -0.004, -0.021, 0.069, -0.015, -0.008, 0.016, 0.003, -0.006, 0.026, -0.021, -0.008, -0.01, 0.035, -0.013, 0.073, -0.055, 0.075, -0.103, 0.031, -0.007, 0.024, 0.059, 0.017, -0.021, 0.055, -0.048, -0.053, -0.026, 0.027, -0.034, 0.031, -0.006, 0.126, -0.011, 0.001, -0.012, -0.011, 0.016, 0.043, 0.013, 0.086, -0.007, 0.02, -0.131, 0.014, 0.01, 0.008, -0.083, -0.017, -0.077, -0.029, 0.054, 0.029, 0.061, 0, 0.066, -0.054, 0.027, 0.045, 0.015, 0.01, -0.013, -0.082, 0.052, -0.024, 0.003, -0.078, 0.046, -0.072, -0.032, -0.054, -0.001, 0.055, 0.004, 0.052, 0.024, 0.048, -0.029, 0.03, 0.048, -0.006, 0.023, 0.032, 0.023, 0.028, 0.054, 0.063, -0.059, -0.007, 0.021, -0.022, 0.045, 0.034, 0.011, -0.002, -0.009, -0.005, -0.057)

nik_close <- c(4792200000, 4755100000, 4335800000, 4267300000, 4251700000, 4174100000, 4145700000, 3798500000, 3795800000, 3734900000, 3723100000, 3468100000, 3461300000, 3459500000, 3455900000, 3436700000, 3432700000, 3428500000, 3402500000, 3393000000, 3390300000, 3376900000, 3340600000, 3335300000, 3318200000, 3307500000, 3291500000, 3283900000, 3272000000, 3256500000, 3239400000, 3235900000, 3230600000, 3226000000, 3199300000, 3191800000, 3175900000, 3169300000, 3158800000, 3155400000, 3151000000, 3133500000, 3132300000, 3125000000, 3114100000, 3101700000, 3095600000, 3093000000, 3089900000, 3047400000, 3039100000, 3038700000, 3011800000, 3006700000, 2991400000, 2979600000, 2975400000, 2962900000, 2938300000, 2927600000, 2922000000, 2916400000, 2908600000, 2905700000, 2889600000, 2850200000, 2840200000, 2825900000, 2821400000, 2816900000, 2809500000, 2767300000, 2760300000, 2759200000, 2749100000, 2738800000, 2736400000, 2736000000, 2726700000, 2715300000, 2713200000, 2699700000, 2699700000, 2691500000, 2687500000, 2680600000, 2675600000, 2668700000, 2664200000, 2663800000, 2658600000, 2655200000, 2646000000, 2638500000, 2635500000, 2633300000, 2606300000, 2597500000, 2585200000, 2575500000, 2572700000, 2571500000, 2563800000, 2560200000, 2559500000, 2551700000, 2548800000, 2547300000, 2530100000, 2526300000, 2493200000, 2486300000, 2480200000, 2475600000, 2467400000, 2457400000, 2450800000, 2443300000, 2440400000, 2430200000, 2429300000, 2415700000, 2403400000, 2389600000, 2371900000, 2344500000, 2337600000, 2330800000, 2326500000, 2300800000, 2278400000, 2276100000, 2230200000, 2222800000, 2207200000, 2178500000, 2153800000, 2145500000, 2143600000, 2103300000, 2093700000, 2086100000, 2085700000, 2068700000, 2062500000, 2032200000, 1981200000, 1973300000, 1956500000, 1923900000, 1882500000, 1876000000, 1872800000, 1840200000, 1837200000, 1822800000, 1807500000, 1790600000, 1782200000, 1779800000, 1754000000, 1732700000, 1704500000, 1696200000, 1675000000, 1666700000, 1665700000, 1637700000, 1617600000, 1616200000, 1614800000, 1607600000, 1606300000, 1601900000, 1588400000, 1582900000, 1561500000, 1555800000, 1539400000, 1539000000, 1534700000, 1529200000, 1523800000, 1515200000, 1513500000, 1484200000, 1481800000, 1458100000, 1454700000, 1447600000, 1446100000, 1437800000, 1436200000, 1435500000, 1433700000, 1432300000, 1406000000, 1400600000, 1397800000, 1396900000, 1396200000, 1392600000, 1390900000, 1388600000, 1387900000, 1386000000, 1377200000, 1373500000, 1373300000, 1369700000, 1364600000, 1362400000, 1357300000, 1356700000, 1347900000, 1345900000, 1340300000, 1339300000, 1313600000, 1305200000, 1284100000, 1282100000, 1276100000, 1275600000, 1274000000, 1273100000, 1258700000, 1235400000, 1231300000, 1195400000, 1187800000, 1173000000, 1168700000, 1148600000, 1133600000, 1108100000)

cor.test(nik_close, nik_vol)

###########################################################################

# STOXX 600 (EUROPE) OUTLIERS #

###########################################################################

stoxx_vol <- c(8068259800, 7557556000, 7243086800, 7130308000, 7015693000, 6784088400, 6569684600, 6532452900, 6506693200, 6455256800, 6441906800, 6300416000, 6260120300, 6189735400, 6170797300, 6047662900, 6041303100, 6016609900, 5990354800, 5920225300, 5814206300, 5810022700, 5783571900, 5778662500, 5776592600, 5731696800, 5715861400, 5715514200, 5685330700, 5667279400, 5664157800, 5644136700, 5601864000, 5598217400, 5596521600, 5530892100, 5481488800, 5447295400, 5391112100, 5329248500, 5288574400, 5284539900, 5162109900, 5156214200, 5155068400, 5141114500, 5120640200, 5109740500, 5108929600, 5061411200, 5044459900, 4898417700, 4851670900, 4829569500, 4761109700, 4727016300, 4717665900, 4668497000, 4665939400, 4636643000, 4634906100, 4626036900, 4563697300, 4559447300, 4558362700, 4537933600, 4493206100, 4457050500, 4428634700, 4414670700, 4414589500, 4403288200, 4396511200, 4378642700, 4375370400, 4371274100, 4370401300, 4369953900, 4324893100, 4315542500, 4272524500, 4219964500, 4209030900, 4190288900, 4167228400, 4136701600, 4120573200, 4080039400, 4010016100, 4001420700, 3994185300, 3990773300, 3963845100, 3962271900, 3935024300, 3914857000, 3913126100, 3873973500, 3844484400, 3822333900, 3806938800, 3765308000, 3756703600, 3747876800, 3727672100, 3725329800, 3687903800, 3686458400, 3675091700, 3673166200, 3655958900, 3623085900, 3593140000, 3529714100, 3472143000, 3429359000, 3364175000, 3353233300, 3227490000, 3214970700)

stoxx_close <- c(-0.018, -0.005, -0.029, 0.063, 0.006, 0.014, 0.011, -0.02, 0.024, 0.064, 0.033, 0.036, 0.009, 0.006, -0.068, 0.016, -0.019, -0.052, 0.119, -0.035, 0.017, 0.069, 0.03, 0.07, 0.008, 0.025, -0.004, 0.002, 0.033, 0.034, 0.019, -0.006, -0.009, -0.095, 0.037, 0.012, 0.053, -0.002, 0.047, -0.006, -0.027, -0.009, 0.003, 0.029, 0.008, -0.028, -0.01, -0.008, -0.003, 0.018, -0.069, -0.009, 0.05, -0.056, -0.021, 0.024, -0.094, -0.011, -0.038, -0.06, 0.009, 0.008, -0.044, 0.013, -0.024, -0.034, -0.013, -0.057, 0.061, 0.016, 0.023, -0.089, 0.017, -0.017, 0.02, -0.014, -0.061, -0.012, 0.063, 0.016, 0.015, -0.041, 0.074, 0.06, 0.034, -0.006, -0.012, -0.013, -0.065, 0.041, 0.001, -0.037, 0.021, 0.035, 0.064, 0.025, 0.02, 0.05, 0.037, 0.042, -0.012, 0.006, 0.003, -0.014, 0.012, 0.049, 0.02, 0.033, -0.025, -0.054, 0.03, -0.028, -0.018, 0.018, 0.028, -0.039, 0.019, 0.018, 0.02, 0.018)

cor.test(stoxx_close, stoxx_vol)

###########################################################################

Additional Findings

There was a negative correlation between the two variables: S&P 500 Monthly Close (n = 218) and S&P 500 Monthly Volume (n = 218). S&P 500 Monthly Close (M = .007, SD = .039), S&P 500 Monthly Volume (M = 77543082110, SD = 18749895626), Conditions; t(216) = -0.34354, p = .73. Pearson Product-Moment Correlation Coefficient: r = -.02.

There was a negative correlation between the two variables: Nikkei 225 Monthly Close (n = 236) and Nikkei 225 Monthly Volume (n = 236). Nikkei 225 Monthly Close (M = .002, SD = .055), Nikkei 225 Monthly Volume (M = 2351271186, SD = 803886229), Conditions; t(234) = -1.2234, p = .22. Pearson Product-Moment Correlation Coefficient: r = -.08.

There was a positive correlation between the two variables: STOXX 600 Monthly Close (n = 120) and STOXX 600 Monthly Volume (n = 120). STOXX 600 Monthly Close (M = .004, SD = .038), STOXX 600 Monthly Volume (M = 4872733427, SD = 1039773116), Conditions; t(118) = 0.31681, p = .75. Pearson Product-Moment Correlation Coefficient: r = .03.

Additional Conclusions

When outliers are removed and the analysis is performed, there is a slight shift in the correlation coefficient values amongst the various indices. S&P 500 (-.14; -.02), Nikkei 225 (-.03; -.08), STOXX 600 (-.18; .03). There also was a shift in correlation significance. S&P 500 (.03; .73), Nikkei 225 (.63; .22), STOXX 600 (.04; .75).

With the removal of outliers, every index had a decline in correlation significance (p), with the exception being the Nikkei 225. Oddly, as it pertains to correlation coefficient values, the S&P 500 rose and remained negative, the Nikkei 225 declined and remained negative, while the STOXX 600 value became positive. 

In almost instance, increases in volume equates for decreases in price. It would seem that the most massive volume increases are the largest contributors to price decline. Seemily, disproportionately so, the Nikkei 500 continues to be an odd duck, in that, it seems to be in a perpetual state of stasis, with smaller upward shifts of volume being more impactful on price than comparatively larger shifts.

Tests for Randomness / Stationarity

Phillips-Perron Unit Root Test

data: sp_vol

Dickey-Fuller = -4.7548, Truncation lag parameter = 4, p-value = 0.01


Phillips-Perron Unit Root Test

data: nik_vol

Dickey-Fuller = -4.2136, Truncation lag parameter = 4, p-value = 0.01


Phillips-Perron Unit Root Test

data: stoxx_vol

Dickey-Fuller = -6.906, Truncation lag parameter = 4, p-value = 0.01


Augmented Dickey-Fuller Test

data: sp_vol

Dickey-Fuller = -2.2459, Lag order = 6, p-value = 0.4725

alternative hypothesis: stationary


Augmented Dickey-Fuller Test

data: nik_vol

Dickey-Fuller = -2.3522, Lag order = 6, p-value = 0.4277

alternative hypothesis: stationary


Augmented Dickey-Fuller Test

data: stoxx_vol

Dickey-Fuller = -2.6845, Lag order = 4, p-value = 0.2921

alternative hypothesis: stationary

Final Thoughts and Conclusions

In every instance, the volume measurements for each index were non-stationary, and non-random. Thus, I suppose that it should be expected, that volume figures should typically increase over time. As was demonstrated by the correlation analysis both as it relates to index/volume assessments (with and without outliers), large unanticipated upward shifts in volume, typically should be expected to cause price decline.

Thus, it might be said, that demand creates its own supply. Or at the very least, impacts supply price in a deflationary manner. Or perhaps some combination of the two.

As it relates to volume’s long term impact on pricing, it would seem that the stationary / random walk analysis that was performed for a prior article, holds true. In that, like a tiny pill bug walking haphazardly across graphing paper, a small push by a human hand here and there may alter the insect’s course, but will otherwise not prove to be impactful, other than demonstrating some significance in the present moment.

In a similar manner, as with a stretched slinky, outside gyrations obviously cause disruption, but only temporarily. Once the interference ceases, the stationarity is maintained.

Markets outside of the United States continue to remain mysterious in comparison to their state side counterparts while comparing growth patterns. Perhaps the limbic bounces of a market’s price have much to do with the culture of an economy. Though, the bounces themselves do remain very much human in origin, regardless. 

The Friendship Paradox

Like many of the critical attributes of life, that which is most evident, lies obscured by monotony. This is especially true as it pertains to mathematical paradoxes, as the most enlightening insights within the field, have the habit of appearing both obvious and universally evident after discovery. Like many mystical traditions, these insights are best discovered through contradiction and reduction.

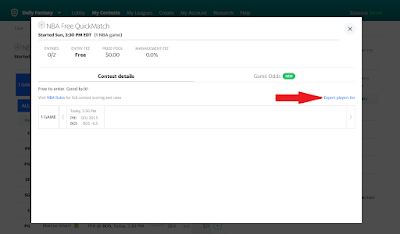
The Paradox

The Friendship Paradox, in simpler terms, identifies the common phenomenon in which an individual, typically possesses less friends than his friends. Additionally, the sum of friends which his friends possess, will be greater than the sum of his total number of friends.

This paradox possesses wide reaching implications, as it describes events which are self-arising and irrefutable. However, before we can detail applicability, we must demonstrate the paradox as it was initially discerned.

First, let’s get some terminology down.

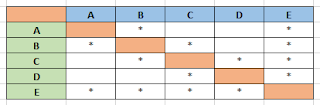
In graph theory, circular graphics are known as nodes, or vertexes. The lines which illustrate relationships between the nodes are known as edges.

Now, let’s utilize this style of graphical representation to demonstrate the relationships between 5 individuals.

The chart below represents the above relationships, but in a different format.

As each relationship is symmetric, if one friend considers himself to be a friend of another individual, that individual also considers the initial individual to be his friend as well. As shown above, A is friends with B and E. B is friends with both A and E, and also friends with C.

If we derive the mean as it relates to the average number of friends that an individual possesses within our experiment, we come to the value of 2.8.

In this instance, E possesses the most friends, and every individual who is friends with E, possesses less. Therefore, the average number of friends that an individual within a group possesses (2.8), will likely be greater than the actual number of friends that a singular individual possesses. 

The Philosophical Implications   

If a single individual begins to quantify a particular phenomenon as it relates to their person on an individualized basis, or even as it relates to a novel phenomenon, then the natural consequence of this endeavor is that this individual from the onset will find himself at a disadvantage.

For example, a new creation upon its genesis, possessing autonomy, will immediately be concerned with attaining sustenance. This was not a concern which was possessed within the prior state of non-being. In contemplating one’s beauty, a young woman immediately begins to compare herself to those whom she perceives as being more beautiful. We would never anticipate the inverse to occur.

This is the paradox of living, striving to possess more while the value of that which we possess becomes diminished. This is due to the passage of time, but also due to singular possession of a resource also diminishing in value. Something within our possession loses value from the moment of possession, as both the individual and the possession are diminished by the natural passage of time.

Example (2):

Here is another example, if an individual walks into a crowded elevator filled with random strangers, then there is a greater probability that this individual will have the same number, or a greater number of friends, than each stranger within the elevator. However, if the same individual were invited to a party hosted by a friend, then there is a lesser probability of this individual possessing more friends, or a similar number of friends, as compared to each other party attendees. In the elevator scenario, there is no guarantee that any individual within the elevator possesses a single friend. This also includes the individual entering the already crowded elevator. However, in the party scenario, each party goer has at least one friend, that being - the party’s host. In this case, the count begins at the neutral value of 1, except for the case of the party’s host, who is friends with every individual in attendance.

As described above, the friendship paradox also seeks to demonstrate, “the sum of friends which his friends possess, will be greater than the sum of his total number of friends.”

In the case of our first example, this value would be calculated as follows:

To better illustrate this phenomenon, I’ve constructed a new example relationship diagram below:

In this instance, E has more friends than A, B, C, D.

E has 4 friends. While A, B, C, D each have 1 friend (E).

In total: A, B, C, D possess the same number of friends in sum (1+1+1+1).

If A, B, C, or D possessed one additional friend – F, then in total, they would together possess more friends in sum than E (1 + 1 + 1 + 2).

If this were the case, the paradox would hold, as E would have a total of 4 friends, but the total number of his friends of friends would be greater (5).

Conclusion

That's all for today.

I hope that you enjoyed this entry and will visit again soon.

-RD

(R) Utilizing Crowd Prediction Methodologies to Draft the Optimal Fantasy Football Team (II)

What would an application be without proof? A notion?

To prove that the ADP drafting strategy is superior to other ranking methodologies, I performed the following analysis.

#############################################################################

Data Source(s):

#############################################################################

ADP

https://fantasydata.com/nfl/fantasy-football-leaders?position=1&season=2022&seasontype=1&scope=1&subscope=1&scoringsystem=2&startweek=1&endweek=1&aggregatescope=1&range=1

Offense

https://fantasydata.com/nfl/ppr-adp?season=2022&leaguetype=2&type=ppr

Kickers

https://fantasydata.com/nfl/fantasy-football-leaders?position=6&season=2022&seasontype=1&scope=1&subscope=1&scoringsystem=2&startweek=1&endweek=1&aggregatescope=1&range=1

DST

https://fantasydata.com/nfl/fantasy-football-leaders?position=7&season=2022&seasontype=1&scope=1&subscope=1&scoringsystem=2&startweek=1&endweek=1&aggregatescope=1&range=1

#############################################################################

The Analysis (n = 300)

#############################################################################

ADP <- c(1.4, 2.4, 2.7, 4.2, 4.9, 5.8, 7, 7.2, 8.8, 10, 10.6, 12.4, 13.1, 14, 15.3, 16, 16.6, 17.9, 18.5, 19.1, 19.6, 19.8, 21.8, 22.7, 24.7, 25.9, 26.1, 27.3, 27.9, 29.3, 30.5, 31.6, 32.4, 33.2, 33.2, 34.1, 36.1, 38, 39.1, 39.3, 39.4, 39.7, 42.3, 43.2, 43.5, 44.2, 45.1, 46.5, 46.8, 47.3, 48.4, 50.2, 50.9, 51.5, 52.2, 53.9, 54.1, 56, 56.7, 57.9, 59.4, 61.2, 61.5, 62.1, 62.9, 63, 63.8, 63.9, 68, 68.1, 69.2, 69.9, 70.1, 71, 71.4, 71.7, 72, 72.9, 75.3, 75.4, 77.1, 77.9, 82.3, 83.8, 84.4, 84.8, 85, 86.7, 87.9, 89.5, 90.2, 90.2, 90.7, 91.3, 91.7, 91.8, 94.4, 95.9, 96.2, 98.5, 98.7, 99.1, 101.9, 102.6, 102.7, 103.6, 103.7, 105.4, 106.5, 106.7, 107.8, 108.6, 109.7, 109.9, 110.6, 111.6, 113.1, 113.6, 113.9, 114.9, 117.3, 117.7, 118.5, 119, 119.6, 120.5, 121, 121.2, 121.3, 122.7, 124.2, 125, 128.9, 129.8, 130.2, 130.2, 130.3, 130.8, 131.2, 132, 135.1, 135.9, 136.1, 136.3, 137.9, 138.9, 140.1, 140.9, 141.8, 142.7, 143.8, 144.8, 145.3, 145.4, 145.7, 147, 147, 148.1, 148.4, 148.9, 149, 149.4, 151.3, 151.4, 152.1, 152.5, 152.6, 153.8, 154.9, 155.6, 155.7, 156.7, 156.8, 156.8, 158, 158.5, 158.8, 158.9, 159.4, 160.1, 160.5, 160.7, 161, 161.5, 162, 163, 163.5, 164, 164.6, 164.6, 165, 165.2, 165.6, 166, 167, 168, 169, 169.5, 170, 171, 172, 173, 174, 175, 176, 177, 178, 178, 179, 180, 180, 181, 182, 183, 184, 185, 186, 187, 187, 188, 189, 190, 190, 191, 192, 192, 193, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265)


PPR <- c(146.4, 356.36, 372.7, 302.76, 368.66, 201.4, 223.46, 237.8, 242.4, 239.5, 211.7, 335.5, 191.1, 316.6, 248.6, 284, 316.3, 301.6, 281.4, 395.52, 168.4, 42, 226.1, 347.2, 216.5, 190.5, 225.4, 185.8, 200.2, 164, 299.6, 75.6, 220.9, 281.26, 141.3, 205.1, 199.1, 229, 417.4, 177.7, 81.2, 176.5, 43.6, 200.5, 180.7, 115.1, 159.4, 259.2, 350.7, 328.3, 167.6, 84.8, 226.8, 236.08, 51.1, 84.9, 98.3, 378.04, 222.8, 145.6, 90.9, 204.2, 216.7, 200.52, 142.7, 52.2, 171.6, 180, 156, 101.5, 126.8, 248.8, 74.2, 166.4, 79, 177.9, 225.76, 267.6, 141.2, 185.3, 249.1, 239.2, 53.5, 246, 87.1, 198.6, 254.6, 271.66, 88.1, 115.6, 227.8, 151.7, 174.8, 105.7, 108.38, 148.7, 69.4, 202.5, 241.9, 88.6, 148.2, 12.46, 168.3, 219.08, 115.7, 178.6, 147.3, 57.3, 87.9, 159.4, 291.58, 55.8, 198.2, 112.7, 237.3, 126, 98.2, 73.5, 135.7, 165.9, 150, 43.4, 135, 105.4, 215.4, 225.9, 70.4, 230.92, 167.12, 139.1, 166.5, 87.7, 88.4, 102, 122.4, 7, 94.1, 114, 105.04, 155.28, 102.9, 160, 103.9, 101.6, 159, 102, 98, 161, 295.98, 295.62, 115, 87.9, 112, 133, 101, 103, 55.2, 43.92, 116, 97, 131, 180.3, 121, 130.6, 143, 142, 119.8, 215.7, 25.5, 125, 123.6, 99, 39, 110, 97.1, 130, 129, 97, 57, 18, 118, 154, 168, 100, 116.9, 20.1, 104, 98.2, 186, 97, 60.2, 110, 101, 52.2, 155.6, 93.8, 3.2, 110, 169.3, 97.6, 34.4, 161.1, 78.9, 25.8, 51.6, 112.3, 115, 176.3, 198.1, 106, 26.4, 82.7, 149.1, 117.8, 88.3, 81.7, 110.1, 83, 4.5, 50.1, 164.1, 73, 12, 57.68, 139, 61.6, 112, 77.4, 45.4, 46.5, 15.1, 35.5, 72.7, 75.2, 84.5, 110, 0.2, 142.1, 34, 12.2, 83, 82.6, 21.1, 77.2, 196.3, 11.4, 51.7, 8.4, 54.1, 161.24, 46.2, 8.6, 8.4, 13.8, 289, 37.8, 170.08, 128.4, 89.6, 112.8, 104.1, 284.32, 154.16, 59.3, 24.9, 114.5, 121.42, 158.5, 59.8, 98.92, 0, 115.1, 10.2, 181.52, 14.8, 4.2, 12.8, 18.8, 103.9, 196.56, 1.3, 11.8, 16.2, 26, 39.1, 43.1, 53.6, 103.8, 27.3, 303.88, 30.8, 64.5, 3.5, 73.88, 110.2, 64.7, 84.3, 30.5, 10.2, 70.3)

cor.test(ADP, PPR)

Which produces the output:

Pearson's product-moment correlation

data: ADP and PPR

t = -13.394, df = 298, p-value < 2.2e-16

alternative hypothesis: true correlation is not equal to 0

95 percent confidence interval:

-0.6791003 -0.5370390

sample estimates:

cor

-0.6130004

#############################################################################

Creating the Visual Output

#############################################################################

my_data <- data.frame(ADP, PPR)

library("ggpubr")

ggscatter(my_data, x = "ADP", y = "PPR",

add = "reg.line", conf.int = TRUE,

cor.coef = TRUE, cor.method = "pearson",

xlab = "ADP (2022)", ylab = "Player Score (PPR)")

#############################################################################

Conclusion

#############################################################################

There was a negative correlation between the two variables: ADP (n = 300), and Player Score (PPR). ADP (M = 134.81, SD = 73.31), Player Score (PPR) (M = 133.33, SD = 86.66), Conditions; t(298) = -13.394 , p < .01. Pearson Product-Moment Correlation Coefficient: r = -0.61.

#############################################################################

As the findings indicate, there is a significant negative correlation as it pertains to ADP and player performance (PPR - 2022 Season). In plain terms, this means that we should typically expect to see better fantasy performance from players with lower ADP rankings. I hope that everyone enjoyed this article and my adherence to APA reporting standards. <3

Until next time. 

Stay cool, Data Heads.

-RD

Utilizing Crowd Prediction Methodologies to Draft the Optimal Fantasy Football Team

To win your league in Fantasy Football, or at least qualify for the playoffs, you don’t need to buy magazines, study tape, or watch ESPN. All that is required, is a general understanding of crowd psychology.

What is ADP?

ADP represents the average draft position for players in fantasy drafts. Each league, for each fantasy sport, typically displays this player value during the drafting process. This value, as the name suggests, is derived from where a particular player was selected by other “fantasy team owners”, during prior drafts.

As was discussed within a previous article demonstrating draft order and its impact on a fantasy team’s final placement, if each fantasy team owner drafted optimally within their respective position, we would expect the final standings to directly reflect the initial draft order.

However, how can an individual be sure that he is drafting optimally? The answer is simpler than one might assume. To achieve optimal drafting potential, one must adhere to drafting players with the best available ADP value throughout the drafting process.

Why does it Work?

Following the crowd consensus, should provide a fantasy participant with their best opportunity for victory. The strictest adherent to this methodology, will benefit most from the number non-adherents within their league. Let’s consider why this is the case.

While pundit, or site rankings of players are often determined by a single individual, or a group of informed individuals, ADP rankings are determined by draft consensus. Meaning, that there are more minds at work as it pertains to determining a player’s draft value. These ranks are also assigned through the drafting process. This differs from other ranking processes, in that, the act of drafting establishes the value. This is similar as to how market participants set prices through buying and selling assets. Whereas, the ranking process is more akin to the way in which planned economies function.   

We’ll assume that ADP perfectly correlates with the eventual points scored by each player within the league. Therefore, with this assumption in place, and also assuming that each league participant drafts optimally, we should expect to see point distributions resemble something like the graphic below. 

(In our example scenario, each subsequent player is valued at one point less than the previous player.)

Therefore, all things being equal, we would expect the final point totals for each league participant to be:

Gaining the Edge

In every instance, the largest advantage belongs to the team which drafts first, with diminishing advantage being assessed sequentially throughout the remaining draft order. To attempt to compensate for this diminishment, or to expand one’s edge regardless of draft position, a league participant should strongly adhere to the ADP value ranking system while drafting. By not attempting to gain an edge through self perceived insight, opportunities will arise as a result of opponents who attempt otherwise.

Every draft misstep is the micro-process of reallocating points from your team to another team within your league. In the example below, the teams highlighted in green are adhering to a strict ADP drafting strategy. The teams highlighted in red, instead are going for a less strict approach.

As is shown in the graphic, the ADP adhering teams were able to benefit from the mistakes made by their opponents. In each instance, the green teams were able to draft the players which were passed upon by their red counterparts. Thus, the ADP adhering teams increased their edge at the expense of the non-adhering teams.

I Know that I Know Nothing

The above strategy, functions on the foundation of two re-enforcing cognitive biases. One being the overestimation of one’s own abilities and talents, and the other being the discounting of the abilities and talents of others.

As far as football is concerned, I have personally witnessed friends who watch far more football than I do, who know far more about the players than I do, blow out their drafts, and fail to make their league’s playoffs in complex and interesting ways. In almost every case, the culprit tends to be impatience and exotic maneuvering. What’s also strange about this cohort of individuals, is that they tend to quickly abandon the strange individualized strategies which initially required a high level of conviction to attempt. This phenomenon itself might warrant an article in the future. 

Be sure to watch the waiver wire, as further edge can be gained from managers who prematurely release underperforming players. Also, it should be noted, that ADP rankings as a drafting criteria, are only applicable in leagues which do not utilize custom rule sets.

Are US Indexes Overweight?

Ever since the COVID Pandemic hit the mainstream news cycle in 2020, I’ve noticed that many of the stocks which I follow seem to dwindle, while the major indexes continue to accelerate upward. I decided to do a bit of research on this subject, and the following is what I discovered along the way.

The Case of the NASDAQ Composite

The NASDAQ Composite is comprised of 3,279 separate equities, each possessing a differing weight as it pertains to their overall contribution to the index’s price. The top 5 equities by weight are:

In sum, 5 equities, and their corresponding evaluations, contribute to approximately 34.07% of the NASDAQ Composite's overall price. 

Over the past five years, the NASDAQ has experienced a hefty appreciation of 67.43%.

However, of this 67.43% evaluation upward, how much of the price shift can be attributed to the top 5 weighted equities from which the index is comprised?

If every other component within the NASDAQ traded completely flat throughout the duration of the previous 5 years, the Dow Jones Industrial Average would have increased in value by approximately 25.51%. As the index appreciated by 67.43%, we can conclude that some of the other components from which the index is comprised, immensely increased the overall potential aggregate (67.43 > 25.51).

Rating: HEFTYCHONK

If 5 companies make up 34.07% of the index’s weight, and 0.15% of the index has increased by approximately 22.51%, while the index itself has appreciated by 67.43%, we can evaluate this furry boi as a Heftychonk.

The Case of the Dow Jones Industrial Average

The Dow Jones Industrial Average is comprised of 30 separate equities, each possessing a differing weight as it pertains to their overall contribution to the index’s price. The top 10 equities by weight are:

In sum, 5 equities, and their corresponding evaluations, contribute approximately 33.38% of the Dow Jones Industrial Average’s overall price.

Over the past five years, the Dow Jones Industrial Average has experienced a healthy appreciation of 32.40%.

However, of this 32.40% evaluation upward, how much of this price shift can be attributed to the top 5 weighted equities?

If every other component within the Dow Jones Industrial Average traded completely flat throughout the duration of the previous 5 years, the Dow Jones Industrial Average would have increased in value by approximately 30.97%. As the index appreciated by 32.40%, we can conclude that some of the components from which the index is comprised, slightly increased the overall potential aggregate (32.40 > 30.97).

Rating: MEGACHONKER

If 5 companies make up 33.82% of the index’s weight, and 16.67% of the index has increased by approximately 30.97%, while the index itself has appreciated by 32.40%, we can evaluate this plump feline as being a MeGaChOnKeR.

The Case of the S&P

The S&P 500 is comprised of 503 separate equities, each possessing a differing weight as it pertains to their overall contribution to the index’s price. The top 10 equities by weight are as follows:

In sum, these 10 equities, and their corresponding evaluations, contribute approximately 30.29% of the S&P 500’s overall price.

Over the past five years, the S&P has experienced a robust appreciation of 52.92%.

However, of this 52.91% evaluation upward, how much of the price shift be attributed to the top 10 weighted equities from which the index is comprised?

If every other component within the S&P traded completely flat throughout the duration of the previous 5 years, the S&P index would have increased in value by approximately 57.35%. As the index appreciated by 52.92%, we can conclude that some of the components from which the index is comprised, actually reduced the overall potential aggregate (52.92 < 57.35).

Rating: OH LAWD HE COMIN

If 10 companies make up 30.29% of the index’s weight, and that 1.98% of the index has increased by approximately 57.35%, while the index itself has appreciated by 52.92%, we can evaluate this rotund hunk of a cat with the phrase, “OH LAWD HE COMIN”!

Conclusion

While every index has been disproportionately impacted by the performance of a few equities, it would appear that the NASDAQ, the index which is least top heavy and possesses the greatest number of companies, has appreciated far more in value than its contemporaries.

Maybe the NASDAQ, though often more volatile than other indexes, benefits from two conflicting attributes. The top 5 stocks within the index anchor the overall price of the index by the magnitude of their market cap, while the much smaller corporate equities, are directionally pressured by component proximity.

Like almost every other medium of existence, it would seem that titans emerge after a certain period of growth. To succeed in such circumstances one must either cast their lot with familiar titans, or learn to swim amongst them.

-RD