Dimension Reduction (SPSS)

This article discusses a topic that I’ve wanted to cover for some time now. Entire books could be written about dimension reduction, and entire books have written on the subject. There is a very good probability, that if you own books that discuss topics such as data mining or machine learning, that dimension reduction is featured somewhere within the text. There are numerous uses for this method. However, what we will be discussing, is a broad overview of the subject matter, and how it is utilized within SPSS.

I should also mention that dimension reduction is rather arduous and complicated if implemented through pen and paper calculations. The reason for such, is that the mathematics that are utilized within this method require an understanding of matrices, an also, with such, necessitate a certain level of tidiness in manual calculation.

I do not expect you, the reader, to understand the underlying methodology, and for that reason, I will not delve into such. Instead, we will discuss dimension reduction as a macro phenomenon, and additionally, we will also delve into the various conclusions that can be derived from the output of the various modeling methodologies.

What is Dimension Reduction?

Also known as factor analysis, dimension reduction is defined by Wikipedia as:

“A statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors.”

What this essentially means, is that the process known as dimension reduction, reduces the number of variables contained within a data set by creating new variables which surmise the original data variables. This can be useful for graphing purposes, as a set such as:

{ 2, 2, 5, 7, 5, 6 }

Could be theoretically reduced to:

{ 5, 3 }

The latter can be represented on a two dimensional plane.

Comparing observations which consist of two dimensional variable representations requires far less effort, and is more efficient from an accuracy standpoint, than the more verbose alternative. Additionally, in creating new variables, the opportunity arises in which a researcher may search for originally unobserved “latent variables”. What this means, is that the new variables, being created in such a manner, may provide insight into the original data, as they may represent macro interactions which were previously unaccounted for. That is to say, that the variables acting in conjunction may represent a larger variable which has not been properly represented.

Now that you have a brief overview pertaining to the subject matter, we will delve into an example which will better illustrate the concept.

Example:

Below is our data set:

From the “Analyze” menu, select “Dimension Reduction”, then select “Factor”.

This should populate the menu below:

Select “Data”, and utilize the top center arrow to designate these values as “Variables”. The selected variables are the values which will be analyzed though the utilization of the “Factor Analysis” procedure.

We will need to specify various options in order to receive the necessary system output. After choosing the “Descriptives” option, make sure that the following selections are specified:

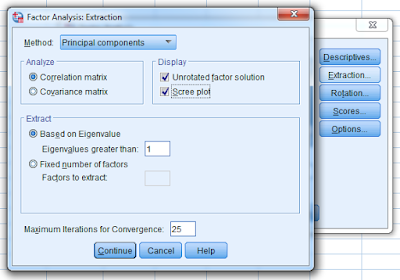
Perform the same steps for “Extraction”:

For “Rotation”, select “Varimax”, as the rotation technique which will be applied to the output data.

We will not be saving the output variables to the data sheet for this specific example. However, if this is an option which you would like to utilize, select “Save as Variables” after selecting the “Scores” menu item.

Once the previously mentioned steps have been completed, select “OK” from the initial menu to produce the system output.

Correlation Matrix – This illustrates the (Pearson) correlation (coefficient) values of the variables within the data set.

Total Variance Explained – This chart seeks to explain the impact of each variable as a component of the larger variable observation matrix. The composition of the values represented within the larger data set are analyzed in order to assess significance as it pertain to eigenvalue and variance. Components which have an eigenvalue above 1 are deemed significant, and are considered necessary components.

Scree Plot – This graph is a visual representation of the data contained within the Total Variance Explained chart.

Component Matrix – The initial algorithm that performed the dimensional reduction procedure identified 4 components that explained 75.116 % of the cumulative variance. These components could qualify as macro variables as they are comprised of varying aspects of the variables which were contained within the initial set. Previously, the term “latent variables” was mentioned. The definition of this term refers to the results produced from component composition process.

Each initial variable, as it is combined to create each component, has a specified impact. For example, within “Component 1”, VarB has a correlated value of .866. Meaning, that whatever VarB represented in the initial data set, its value is most represented within “Component 1” as compared to the additional variable values. In an inverse manner, within “Component 1”, VarC’s value is negatively correlated in the way in which it is associated with the other variables within “Component 1”.

Attempting to clearly define the phenomenon that each component variable is associated with from a macro level perspective, can lead to insight as it pertains to the original data set and the initial variables.

Rotated Component Matrix – The concept of rotation as it pertains to components is incredibly complicated when expressed mathematically. In summarization, what rotation achieves when applied to an existent component matrix, is a shifting of previously established components, in order to reduce spatial distance without disturbing component ratios.

There are various rotational options available within SPSS which are applicable to varying data types.

The two different categorical methods of rotation type are:

Orthogonal – This method is utilized when the variables which will be analyzed are not highly correlated.

Oblique – This method is utilized when the variables which will be analyzed are highly correlated.

The rotational methods which are available within SPSS to perform rotation are:

Varimax – (Orthogonal) The most popular rotational method, at least, as it pertains to research

literature. This method was synthesized to simplify the interpretation of component factors. This is achieved through minimizing the number of variables that have high loadings on each factor. What this essentially means, is that variables with a high correlation are reduced within the synthesized component. To offset this reduction, variables with lower correlations are increased. 

Direct Oblimin Method - (Oblique) Another popular rotational method. A “delta” variable is utilized to achieve the results which are provided by this methodology. The default value for this variable within SPSS is 0.

Quartimax Method – (N/A) This rotation method seeks to minimize the number of variables needed to define a component.

Equamax Method – (N/A) A method which consists of the combination of the varimax and the quartimax methodologies.

Promax Rotation – (Oblique) A somewhat simplified variation of the direct oblimin method. This method is useful for larger data sets as it can be calculated more rapidly that the direct oblimin method.

Conclusions

So what is the purpose of performing this intense and involved analysis? In my opinion there are two fundamental reasons. The first of which refers back to the concept of “latent variables”. By deriving components which are comprised of aspects of the original variables, more encompassing macro phenomenon can be derived, and subsequently analyzed. The second fundamental reason for performing this analysis is to achieve dimensional simplification.

Reducing dimensionality allows for more accurate measurements of Euclidean distances between points. Data can only be visualized in three dimensions, however, typically two dimensional graphs are the standard as far as visualization of data is concerned. Though the default setting within SPSS is established to select the number of components to include within the final model, there is an option which allows the user to make the initial decision. Through the utilization of manual determination of component inclusion, we can achieve a three dimensional model, from which an additional model may be derived.

In the next article, I will continue to discuss the concept of dimension reduction. Additionally, in such, I will be specifically discussing the topic of "Nearest Neighbor Analysis". The combination of these two subjects will further illustrate what was discussed in this article, and also elucidate the premises of dimensionality and Euclidean distance.